The Verdi Tuning Forks
Return to the Verdi Tuning! Beauty and harmony applies to music, healing, science, and life in general. To save the health of singers’ and prevent damage to instruments, the great Classical composer Giuseppe Verdi insisted that the A above Middle C be a 432 Hz, over a century ago. Happily, and finally, now in the 21st century, this is catching on internationally. SWB 256 Verdi Tuning Forks feature the C octaves of 128 Hz, 256 Hz (Middle C), 512 Hz and the Verdi “La” at 432 Hz. Order individual tuning forks or any of our Verdi Set combinations. Mix and match, and stay in tune and be harmonic with the Verdi Tuning.
-
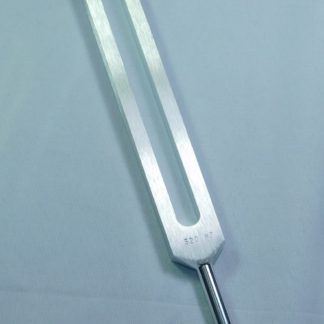
E=320 or 324 Hz Tuning Fork
$36.99 -

Verdi Set of 3 Plus 1
$117.00 -

Verdi Set of 3 Plus Soft Rubber Hammer in Pouch
$95.00 -

C=128 Hz Verdi Tuning Fork – Weighted
$38.99 -

A=432 Hz Verdi Tuning Fork
$26.99 -

C=256 Hz and G=384 Hz Verdi Tuning Fork Pair in Pouch
$72.00 -

C=256 Hz Verdi Tuning Fork
$34.50 -

C=512 Hz Verdi Tuning Fork
$36.99 -

G=384 Hz Tuning Fork
$36.99 -

Verdi Set of 3 Tuning Forks 256, 432, 512 Hz
$75.99 -

Verdi Set of 3 Tuning Forks plus Weighted C128 Hz in Fabric Pouch
$128.00 -

Verdi Tuning Scale in Pouch
$214.00 – $229.00
